Die Kreiszahl PI:
Die Kreiszahl Pi ist für viele ein Geheimnis, sie wissen nicht wie diese eigentlich „genau“ berechnet wird.
Es ist allerdings nicht so schwer, sie tatsächlich zu berechnen oder besser gesagt sich zu nähern, denn wie man weiß, ist die Kreiszahl eine irrationale Zahl, mit unbestimmt vielen Kommastellen.
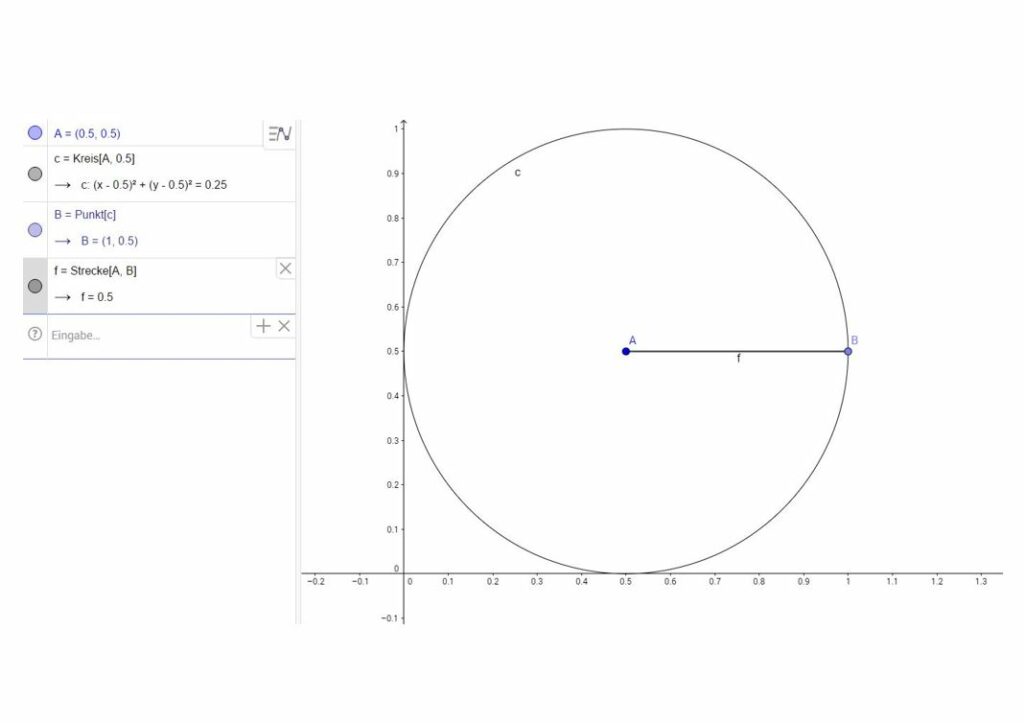
Man nehme einen Kreis mit dem Durchmesser 1, also der Radius ist 0,5.
r = 0,5 – die Formel 2r x π = U (Umfang des Kreises)
Jetzt haben wir 2 r ist 1, also 1 x 3,141… = 3,141…
Wir müssen beim Berechnen also auf die Summe 3,141… kommen, wie geht das?
Eigentlich ganz einfach mit Trigonometrie, wir zeichnen also Dreiecke in den Kreis ein.
Wir zeichnen so viele Dreiecke wie möglich in den Kreis ein, denn umso genauer lässt sich die Kreiszahl danach berechnen.
Grundsätzlich weiß man, dass sich gleichschenklige Dreiecke schwer berechnen lassen, wenn man keinen Winkel hat. Wir wissen, die Seiten des Dreiecks haben immer 0,5 Länge, aber wir haben keinen Winkel – was tun?
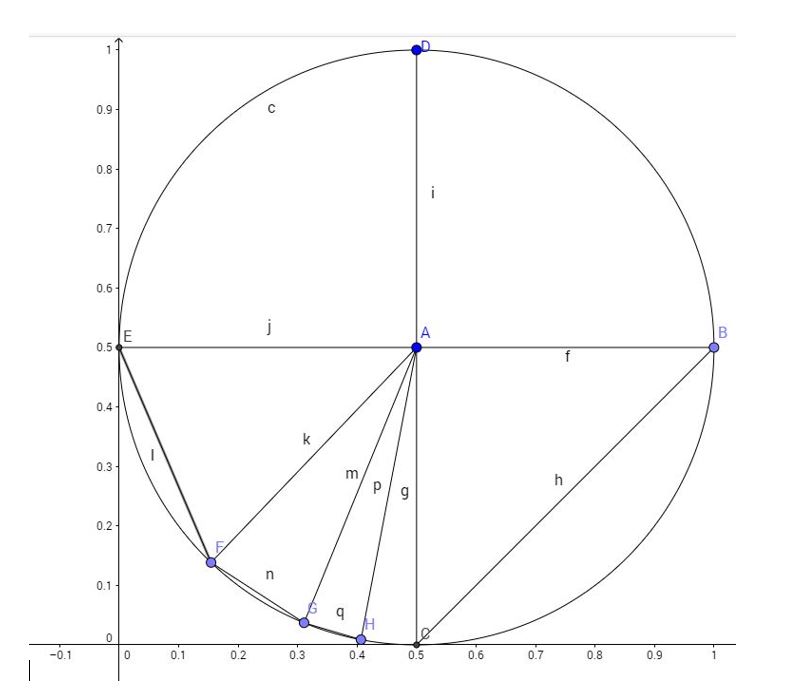
Ganz einfach, wir zeichnen in das gleichseitige Dreieck in der Mitte einen Strich und machen es somit zum rechtwinkeligen Dreieck, das sich mit der bekannten Formel a²+b²=c² berechnen lässt. Außerdem können wir davon ausgehen, dass das erste große Dreieck 45° hat, in dieses ziehen wir eine Linie und wissen, das nächste hat 22,5 ° und wir können dieses wieder halbieren und wissen es werden 11,25° sein usw.
Grundsätzlich brauchen wir nur den Sinus aus α um die Gegenkathete zu berechnen.
Sin α = Gegenkatete/Hypotenuse
Sin α haben wir, die Hypotenuse haben wir auch, die ist ja 0,5
GK = sin α x Hypotenuse
und schon haben wir die Gegenkathete, das ist nun die Länge, die wir brauchen um den Umfang zu berechnen.
Wenn man den Kreis in 128 Teile zerlegt, bekommt man schon die ersten drei Kommastellen, probiert es aus, es macht Spaß, ihr werdet sehen.
Das ist allerdings nur eine Methode, wahrscheinlich die einfachste und der Artikel soll nur dazu beitragen, sich etwas mit Mathematik zu beschäftigen.
